Improving Digital Asset Security

by Deepak Maram (Mysten Labs, IC3 Alum), Mahimna Kelkar (Cornell Tech, IC3) & Ittay Eyal (Technion, IC3)

Long-time Bitcoin developer Luke Dashjr lost a large number of Bitcoins to a hacker, who apparently gained access to Luke’s private key. In the March 2022 Ronin hack an attacker took $600M worth of assets after compromising several private signing keys. And there’s this story of one friend who resorted to hypnosis hoping to recall a forgotten private key. The common theme: Securing digital assets is hard, whether you are an individual, even a pro, or a major entity. To get better at it we present a formal model to reason about the problem and tools for evaluating security.

Broadly, the problem is that of authentication. Authentication is everywhere. One example is personal cryptocurrency assets (self-custodied with standard wallet software). It is possible to keep a secret key in 5 locations (for redundancy); or keep 5 secret keys and use 3-out-of-5 signatures (e.g., Casa). Another example is institutional crypto holdings (bespoke wallet); here some use a multi-sig hot wallet for a smaller amount in daily operations and a larger amount secured with a “very secret” key in an extra strong vault with armed guards. Outside of the crypto world, there are large-scale centralized authentication schemes, e.g., used by your favorite social network, namely password, or sometimes a password plus a one-time code from a dongle or an sms. More recently, we are witnessing a switch to WebAuthn (e.g., deployed on the Sui blockchain) which uses public-key crypto with the user’s secret key stored on their own device’s trusted hardware.

But when stakes are particularly high, we observe an additional design pattern. For example, some banks send an email notification allowing the user to abort a transaction within a certain period of time. The key idea is the use of delays to undo a transaction within a given period of time. Intuitively, delays help when the mechanism can reach out to the true user before taking any sensitive action that would otherwise have been irrevocably executed. We refer to this design pattern as interaction and mechanisms that leverage it as interactive authentication mechanisms.

As we have seen, authentication is everywhere, and it is critical. But its design is often heuristic, using sub-optimal solutions. In particular, many mechanisms deployed today do not make use of interaction. To give an example, a commonly recommended cryptocurrency wallet design is a k-out-of-n mechanism, which is one-shot and lacks any interaction. We will see the significant gap in security levels attained by simple one-shot mechanisms like the 1-out-of-2 or 2-out-of-3 mechanisms and the new interactive mechanisms we propose.

Our main contribution is a theory of interactive authentication mechanisms allowing (a) mechanism designers to formally model their mechanisms and analyze their security, and (b) provide a common framework to compare the security level of different mechanisms, both interactive and one-shot. In addition, we discover two classes of interactive mechanisms, called priority and majority mechanisms. We prove that these mechanisms achieve maximal security, that is, no other mechanism can achieve better security than these.

We’ll go over a use case before getting formal and moving to general results. We analyze an interactive mechanism employed by a leading bank used by over 100 million users and show how our new mechanisms can improve its security.

Improving security of a popular bank’s login mechanism

Take the case of an authentication mechanism employed by the largest bank in India, HDFC. The bank requires the user to set up a second factor via a phone message. When sending money to a new account, one to which money has never been sent before, the bank requires the user to (a) first authorize with both the factors, password and a OTP received on phone and (b) wait for 30 mins during which the process can be canceled (with just a password). The rationale behind their ad-hoc interactive mechanism, as stated on the bank’s website is: “we introduced the concept of an additional 30 minutes cooling period after beneficiary addition. In this time period, we send SMS and Email alerts of the beneficiary addition, which gives the customer time to review the payee if fraudulently/erroneously registered”

At a first glance, it may seem natural that having such a cooling period increases the security. Even if an attacker gains access to both the password and the second factor, the attacker needs to wait for 30 minutes before it can withdraw money. This extra time allows the user to cancel the new beneficiary addition process.

But in reality, the cooling period does not improve security because an attacker can instead do the following. HDFC allows changing the password with just the second factor, in a process that can be finished instantaneously. So an attacker that gains access to the mobile phone can first change the password, and now that it controls both factors, it can proceed to withdrawing money. Note that the user cannot cancel the beneficiary addition process without knowing the password.

Put simply, the HDFC bank’s mechanism is overly dependent on the security of the second factor. The scheme becomes insecure as soon as an attacker gains access to it.

How to improve HDFC?

First note that if the attacker somehow gains access to both the password and the second factor, there is not much we can do as the attacker knows all the credentials used. But can we secure HDFC if the second factor is leaked (both parties know it) but the password is safe (only the user knows it and the attacker doesn’t)? That would clearly improve the security of the HDFC mechanism as attacks that only target the second factor may not be enough to steal money.

Our idea is to employ the following mechanism before a password reset:

1. Any party can initiate the mechanism by submitting non-zero credentials, e.g., only password or only the second factor or both. Denote the set of credentials submitted by the initiator (player 0) as C0.
2. The mechanism enters a cooling period of, say, 30 mins (this makes the user experience slightly worse compared to the existing mechanism)
3. Any party (player 1) can submit a non-zero credential set C1 to try and stop the password reset before the cooling period expires.

Note that the real user can be either player 0 or 1 and the bank doesn’t know which. After the cooling period ends, the bank decides whether a password reset happens or not by comparing the two sets of credentials using the below table. Note that P0 wins => password reset and P1 wins => password reset canceled.

Observe that in the scenario of a leaked second factor and a safe password, the attacker is not able to reset the password anymore (assuming player 0 is the attacker, this scenario corresponds to the third row). In essence, the introduction of a cooling period provides the user enough time to respond with both the credentials.

Also notice how we prioritize the second factor (mobile credentials) over a password in the above table (see the last two rows). The above mechanism is an instance of a general class of mechanisms we uncover called “priority mechanisms” (more on them below). Further security improvement is possible by adjusting the priority to the relevant context. Say that we assume passwords are less likely to be stolen (only the attacker knows it but the user doesn’t) than the second factor. In this setting, it is more secure to employ a different priority mechanism where passwords are assigned higher priority than second factors, i.e., switch the winner in the last rows of the above table.

Capturing a mechanism’s security level

Let us now take a broader view of the problem. So far, both the academic and industrial discourse around the security of a multi-credential authentication mechanism have often been a bit vague. In contrast, a lot of work has been done analyzing the security of individual credentials, e.g., passwords. For example, we often hear people say that some mechanism (e.g., multi-sig or a 2FA) offers better security than another (e.g., say a single key or a password) based on some intuitive reasoning. We show that by rigorously analyzing the problem, it is possible to accurately compare mechanisms and find significant improvements that are otherwise hard to see.

Our model works as follows. Any authentication mechanism uses one or more credentials to identify the user. The definition of a credential is purposefully vague: it can be anything, e.g., passwords, OTPs, biometrics, etc. We have two players: a user and an attacker. We say that the mechanism succeeds if the user authenticates and fails otherwise.

Each credential is said to be in one of four states based on which party has access to it:

If there are n credentials in total, then at any given point of time, we are in one of 4^n scenarios as defined by the states of these n credentials.

A mechanism’s security profile is the subset of the scenarios in which the mechanism succeeds, i.e., the user wins. Put differently, we evaluate the performance of the mechanism in all the 4^n scenarios and find where it succeeds. For example, the 1-out-of-2 mechanism (OR wallet) fails if one of the credentials is leaked or stolen (as the attacker knows one of the two credentials). So looking at a mechanism’s profile gives a complete picture of the mechanism’s security in all possible scenarios.

Comparing the profiles of two different mechanisms, we can order mechanisms as follows:

1. Mechanism M1 is better than M2 if the profile of M1 is a superset of M2
2. Mechanism M1 is equivalent to M2 if they have the same profiles.
3. Mechanism M1 is incomparable to M2 if the profiles of M1 and M2 do not satisfy a superset or subset relation.

How to DOUBLE the security of your cryptocurrency wallet?

Today, arguably, the most popular method to improve wallet security is to use multiple credentials combined via a threshold (e.g., k-out-of-n). We see this design natively supported by many blockchains, e.g., Bitcoin, Sui, and employed in popular wallets, e.g., Gnosis Safe, Argent, Casa, BitGo.

We are now ready to see how to improve security with an interactive mechanism. Specifically, the priority mechanism introduced before achieves better security than these commonly used mechanisms. For example, let’s look at the case of just two credentials c1 and c2 and compare three wallets: (i) AND wallet: A popular way of combining two credentials that require both the credentials, (ii) OR wallet: Another popular way of combining two credentials that require either of the two credentials, (iii) Priority mechanism: our novel mechanism introduced before. We look at all the one-safe scenarios (scenarios where one of the credentials is safe) and note whether the given mechanism succeeds or fails.

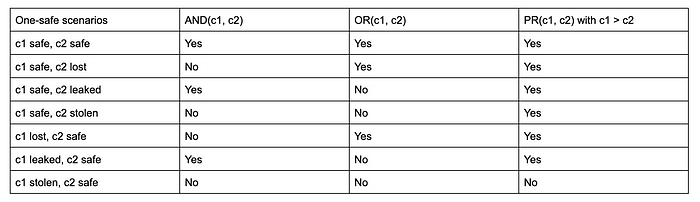
As one can see, the priority mechanism succeeds in six scenarios and is better than both the AND and the OR wallets. Or put differently, the priority mechanism’s profile is a superset of the profiles of AND and OR wallets!

A similar story plays out in the case of three credential mechanisms too. The popularly used 2-out-of-3 mechanism (submitting any two out of the three credentials succeeds) succeeds only in 14 scenarios (its profile is in Table 8 of our technical report). In comparison, the 3-credential priority mechanism succeeds in 28 scenarios! However, it turns out that the 3-credential priority mechanism and the 2-out-of-3 mechanism are actually incomparable to each other (the 2-out-of-3 mechanism succeeds in all scenarios where two of the credentials are safe and the third is stolen but the priority mechanism fails when the highest priority credential is stolen).

Not to worry, we find another class of mechanisms called majority mechanisms. They behave very much like the priority mechanisms except they take a different route to determine the final winner after all players have submitted their credentials. Majority mechanisms judge the player that submits the most credentials as the winner, with a tie-breaking function in case the result is a tie. The 3-credential majority mechanisms also succeed in 28 scenarios like the priority mechanism. And it is better than the 2-out-of-3 mechanism (profile is in Table 1 of the report).

An overview of our theoretical results

Let’s take a look at some of our key results. To start off, we use finite automata to model authentication mechanisms; state transitions are induced by the showing of credentials by a party or the passing of time. Adopting such a general computational model allows us to prove some general results.

We find that priority and majority mechanisms are always maximal: For any number of credentials, given a priority or a majority mechanism that succeeds in certain scenarios, there is no mechanism that succeeds in all these scenarios and more. To prove this, we rely on two key lemmas that are both instructive by themselves:

1. No mechanism can succeed in a “bad scenario” where all the credentials are leaked, lost, or stolen.
2. If a mechanism succeeds in a scenario S1, then it must fail in its complement, where a complement scenario inverts the credential availability, that is, it switches safe and stolen credentials. E.g., if S1 = (c1 safe, c2 leaked, c3 stolen), then S1’s complement is (c1 stolen, c2 leaked, c3 safe).

These two lemmas allow us to prove that there cannot exist an n-credential mechanism that succeeds in more than (4ⁿ-2ⁿ)/ 2 scenarios. For example, setting n=2 we get 6 and when n=3 we get 28, the same number of scenarios achieved by the priority and majority mechanisms, making them maximally secure.

For n = 2,3, we also identify a complete maximal set of mechanisms, composed of priority and majority mechanisms plus an additional type we call priority with exception. This set has a unique property that makes it interesting: “any other n-credential mechanism is either equivalent or worse than some mechanism in a complete maximal set”. In other words, for a given n, this set contains all the mechanisms you ever need to care about as far as security is concerned. Specifically, for any probability distribution of credential faults of n=2,3 credentials, there exists a mechanism in the complete maximal set that achieves the optimal security.

In more detail, we find that the complete maximal set for n=2 is of size 1 (just the priority mechanism), and for n=3 is of size 14. You can find Python code at https://github.com/mskd12/interactive-authentication that allows you to find the best mechanism (from the complete maximal set) for a given probability distribution.

Key Takeaways

If you want to take away just one thing from this article, then let that be that the use of interactivity significantly increases security of authentication mechanisms.

This type of interaction crucially relies on a communication channel between the mechanism and the user. Today, the primary mode of communication used by most existing mechanisms are either email, text based notifications or sometimes physical mail (think banking and national authorities). But a lot more can be done to make existing notification channels more robust. For example, making sensitive notification messages sticky for a short period of time so that even an attacker that has access to your device cannot delete those can help.

We discover two novel classes of interactive mechanisms: priority and majority mechanisms, that are both easy to understand, deploy and are maximally secure.

It is worth noting that the main downside of interactive mechanisms is that they do not decide instantaneously, posing a slight usability challenge. This makes them useful in settings where the demand for security outweighs other concerns. Formalizing usability considerations is also an important direction for future work, e.g., can we design maximally secure mechanisms where the user need not submit too many credentials or wait too long?

For more details, please see our technical report at https://eprint.iacr.org/2022/1682 (recently published at CCS’24), https://github.com/mskd12/interactive-authentication for the associated code, and do not hesitate to reach out to the authors with any comments or questions.

Deepak Maram: sm2686@cornell.edu @mskd96

Mahimna Kelkar: mahimna@cs.cornell.edu @_mahimna

Ittay Eyal: ittay@technion.ac.il @ittayeyal

PS: We also analyze a past version of the Argent cryptocurrency wallet (authors have no personal interest; their design has since changed), one of the most complex interactive mechanisms we’ve encountered in the wild, and identify many concrete improvements. Details can be found in the technical report.

Editor: Bria Han (IC3 Community Manager, jh2584@cornell.edu)